The shape of a rectangular tank is that of a rectangle or cuboidal. Thus, the formula for volume or capacity of a rectangular tank can be calculated in a similar way to that of the volume of a cuboid or a rectangular box. The volume of a rectangular tank is represented in cubic units. Length times width gives the surface area of the pool. Multiplying that by the average depth gives the volume in cubic feet.
Since there are 7.5 gallons in each cubic foot, multiply the cubic feet of the pool by 7.5 to arrive at the volume of the pool . With this volume of a rectangular prism calculator - a.k.a. a box volume calculator - you'll find the volume of any box-shaped container in a blink of an eye. You need to enter only three values, and we'll calculate the volume for you (though it's not so tricky, you could figure it yourself😊). If you're searching for the definition, check the section What is a rectangular prism. Make sure to use the actual water depth in your calculations, not the depth of the container. For example, the hot tub depicted in Figure 2 is 4 feet deep, but the water is only filled to about 3 feet.
Using 4 feet in this calculation will result in a volume 33 percent greater than the actual amount of water. This could mean serious errors when adding chemicals for example, which are administered based on the volume of water in question. There might be a time when you want to know the potential volume, if filled to the brim. Then, of course, you would use the actual depth measurement. Multiplying that by the depth gives the volume in cubic feet.
Since there are 7.5 gallons in each cubic foot, multiply the cubic feet of the pool by 7.5 to arrive at the volume of the pool, expressed in gallons. The volume of a rectangular tank is defined as the amount of liquid that can be held by the rectangular tank. The rectangular tank has a length, breadth, and height which a cuboid in shape.
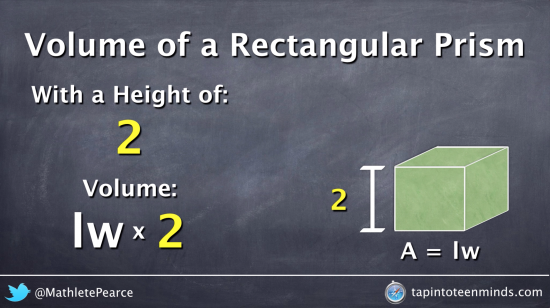
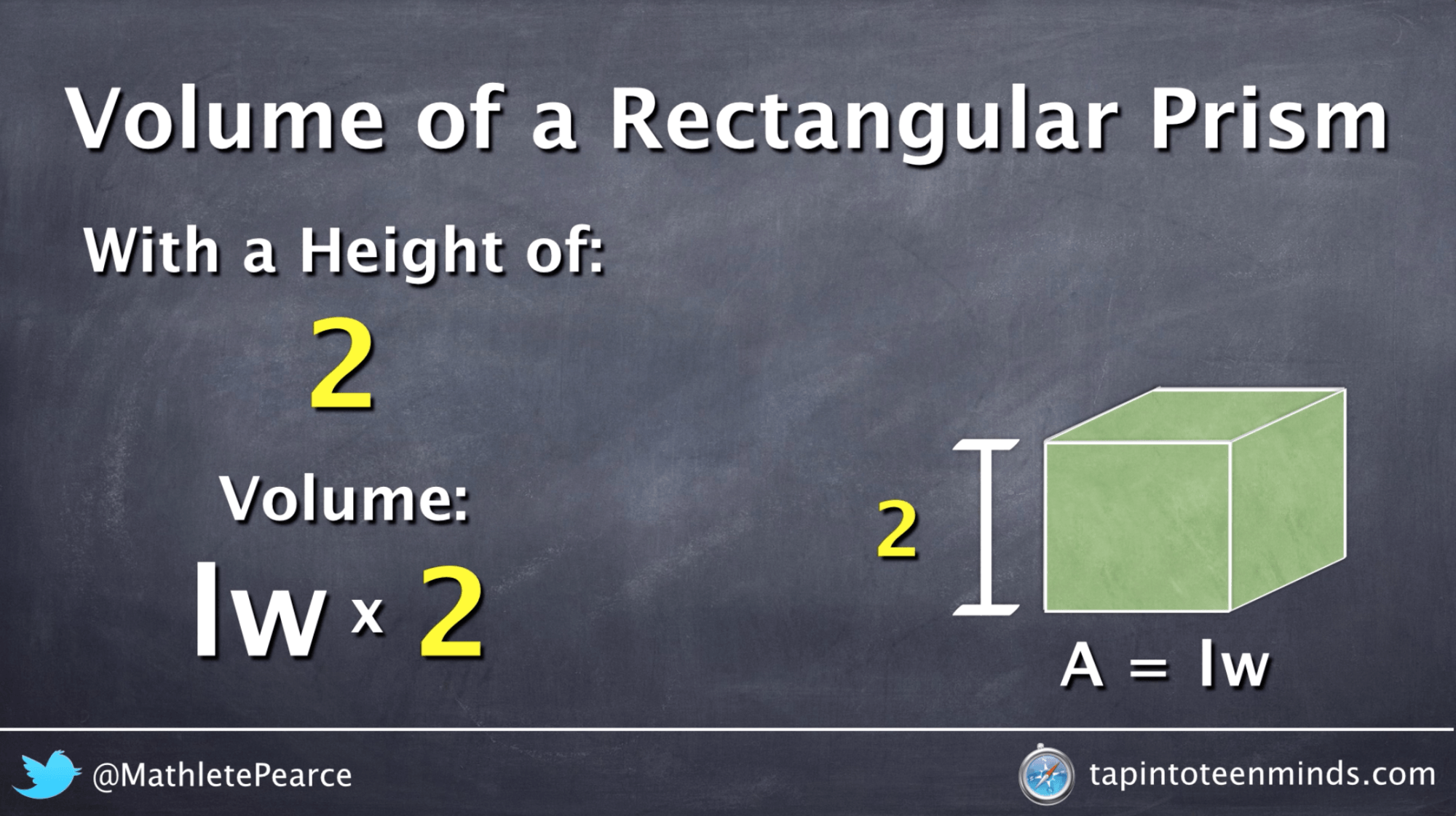
This tank is a three-dimensional shaped object whose volume is given in cubic units, that is m3, cm3, in3 or ft3, etc. As the rectangular tank is three-dimensional thus, the volume of the rectangular tank also lies in a three-dimensional plane. The volume of a rectangular tank, i.e, the capacity of the rectangular tank, can be calculated by finding the volume of the cuboidal structured tank. Let the area of a rectangular base be "A", the height of the tank be "h" and the volume of the rectangular tank be "V".
Then, the volume of the rectangular tank is given by multiplying the base area and height. The methods below will give you cubic measures such as ft3 or m3 depending on your units of measure. If you're calculating filled tank volume by hand using these methods you can covert cubic feet to gallons, and cubic meters to liters using our Volume Conversion Calculator. There are two methods used to calculate the capacity of irregular shapes. First, you can imagine the pool or hot tub as a combination of smaller, regular shapes.
Measure these various areas and use the calculations described previously for each square or rectangular area and for each circular area. Add these volumes together to determine the total capacity. Ften, in the United States, the volume of a liquid is measured in gallons, such as milk. Select the style of tank and its dimensions to calculate the capacity in gallons and liters.
Optionally, enter the filled depth to calculate the volume of liquid in a tank. Ou can measure from the inside of the tank or, if preferable, measure the outside and then subtract the width of the tank walls to determine the inside measurement. Next, multiply the length, width and depth measurements in order to find the cubic volume in cubic inches. Capacity calculations involve calculating surface area and volume of the pool or spa. This article describes in detail how to calculate the size and capacity of the pool you are planning.
Well, now that you know what a rectangular prism is, and its volume formula, all the calculations should be a piece of cake! Just measure the three dimensions of your rectangular prism, and use the method from the previous paragraph. Alternatively, you can simply use our box volume calculator.
If you don't know how many gallons a tank can hold, you can calculate it yourself using a simple formula. The measurements you need to calculate the volume are different, depending on the tank you have. Rectangular tanks, like aquariums require one formula, while cylindrical tanks, like drinking water tanks, require another.
Here is a great tool to calculate the volume or capacity of your pool. Remember to measure from the depth of the water rather than the height of your wall. It's in a regular box shape, nothing fancy, like a corner bow-front aquarium.
If you're wondering how much water you need to fill it, simply use the volume of a rectangular prism formula. It is a similar story for other pets kept in tanks and cages, like turtles or rats - if you want a happy pet, then you should guarantee them enough living space. For example, if the measurements are 20 inches by 12 inches by 12 inches, the volume is 2,880 cubic inches. Tank volume calculations are based on tank geometries shown below. These tank shapes are calculated assuming exact geometric solid shapes such as cylinders, circles and spheres.
Actual water and oil tanks may not be perfect geometric shapes or might have other features not accounted for here so, these calculations should only be considered estimates. The flow-rate of a river, or of a canal, is the volume of water discharged through this river, or this canal, during a given period of time. Related to irrigation, the volume of water is usually expressed in litres or cubic metres and the time in seconds or hours . The volume of a rectangular box is the amount of space occupied by the object.
This is an online volume of a rectangle calculator that calculates the volume of a rectangular box from the dimensions of length, width, and height. A Rectangular box is a geometrical figure bounded by six quadrilateral faces. In measuring the capacity of a circular spa, you might need to calculate two or three areas within the hot tub and add them together to arrive at a total volume. An empty circular hot tub looks like an upside-down wedding cake, because of the seats. Therefore, you might want to treat it as two separate volumes-the volume above the seat line and the volume below.
In the wooden hot tub, where there is actually water above and below the seats, the tub can be measured as if there are no seats because this difference is negligible. If most of the pool is only 3 or 4 feet and then a small area drops off suddenly to 10 feet, you will have a different average depth. In such a case, you might want to treat the pool as two parts. Measure the length, width, and average depth of the shallow section, then take the same measurements for the deeper section. Calculate the volume of the shallow section and add that to the volume you calculate for the deeper section.
The resulting tank volume will be in the cubic form of the initial measurements. For instance, if the initial tank measurements were in inches, then the volume measurement would be in cubic inches. Enter U.S. dimensions in feet or inches , or metric dimensions in meters or centimeters . Results are presented in U.S. fluid gallons, Imperial gallons, cubic feet (ft³), metric liters and cubic meters (m³).
The cubic volume can be calculated by including the depth of the pool with the surface area. For accurate calculations, the pool should be divided into various areas according to the depth. However, when calculating the volume of a rectangle attached to a triangle, find the area of the base and multiply it by the height. The area of the base is found by multiplying the length by the width of the rectangle. The filled volume of a rectangular tank is defined as the space occupied by any liquid in the tank. Calculate the filled volume of a horizontal cylinder tank by first finding the area, A, of a circular segment and multiplying it by the length, l.
Estimate the total capacity and filled volumes in gallons and liters of tanks such as oil tanks and water tanks. The surface of these triangles is expressed in square centimetres . Surface areas can also be expressed in square decimetres , square metres , etc... However, one gallon of chlorine, for example, poured into one million gallons of water does not equal 1 ppm. That is because the two liquids are not of equal density.
This becomes obvious since a gallon of water weighs 8.3 pounds but a gallon of chlorine weighs 10 pounds . The chlorine is a denser liquid; there's more of it than an equal volume of water. Volume is the amount of three-dimensional space taken up by an object.
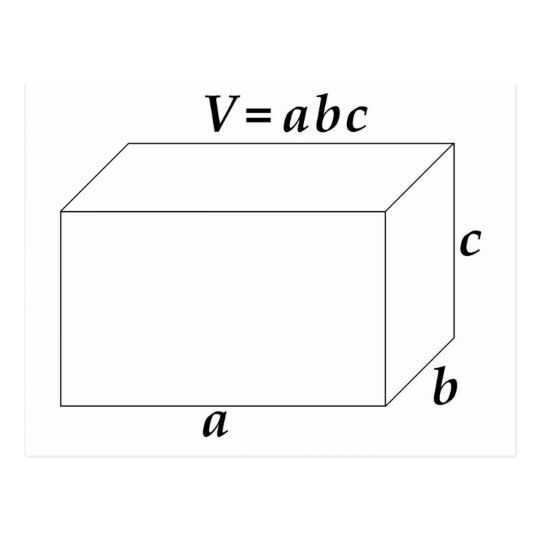
The computer or phone you're using right now has volume, and even you have volume. Finding the volume of a rectangular prism is actually really easy. Just multiply the length, the width, and the height of the rectangular prism. This article will walk you through the process step-by-step and show you an example. The first step is to measure the key dimensions of the tank. For round tanks, find the diameter and length or height.
For rectangular or cubes, find the length, width, and height. You can find the volume or capacity of a tank in a few easy steps. Of course, the calculator above is the easiest way to calculate tank volume, but follow along to learn how to calculate it yourself. Suppose it is necessary to make a graph of the growth rate of a maize plant. The basic unit of volume in the metric system is the cubic metre which is obtained by multiplying a length of 1 metre, by a width of 1 metre and a height of 1 metre (see Fig. 16). The number 3.14, refers to pi, which is a mathematical constant.
The radius is one-half the diameter, so measure the distance across the broadest part of the circle and divide it in half to arrive at the radius. Squared means multiplied by itself, so multiply the radius by itself. For example, if you measure the radius as 5 feet, multiply 5 feet by 5 feet to arrive at 25 feet. There are situations where you will need to calculate the volume of a triangular prism. This could include a triangular section on a concrete slab or the excavation of soil from a sloping block.
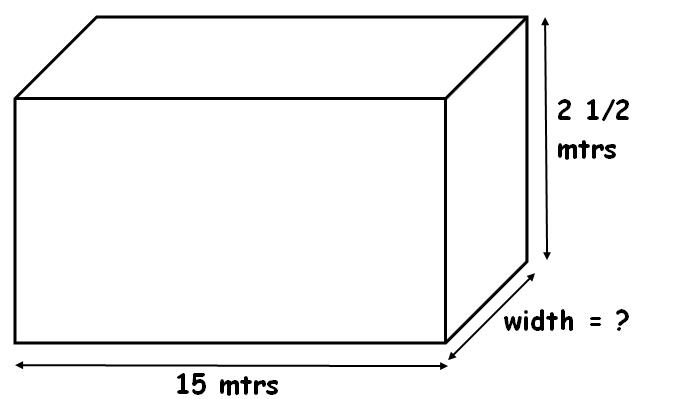
A rectangular prism has a width of 3 inches, a length of 6 inches, and a height triple its length. No, the order of height, width, and length does not matter because we need to multiply all three quantities to determine the volume of a rectangular tank. As multiplication is commutative, thus, the product of the three quantities will always result in the same value irrespective of their order.
Therefore, the volume of the rectangular tank is 1200 unit3 and the filled volume of the rectangular tank is 800 unit3. For example volume 24 could give the length, width, and height of 2, 2, and 6; or 2, 3, 4; or 1, 1, 24; and so on. Thus, the final step is to convert from one volume measurement to the desired unit of the result. Try our volume converter to convert the results to gallons, liters, or any other unit.
A rectangular prism is a 3D shape with 6 faces, all of which are rectangles. Other names for a rectangular prism are a cuboid, or simply a box. Suppose there is a reservoir, filled with water, with a length of 5 m, a width of 10 m and a depth of 2 m. All the water from the reservoir is spread over a field of 1 hectare. The volume of this block is expressed in cubic centimetres . Volumes can also be expressed in cubic decimetres , cubic metres , etc.
The most common shape of a canal cross-section is a trapezium or, more truly, an "up-side-down" trapezium (see Fig. 10). Thus, we follow the steps shown below to find the volume of the rectangular tank. There are three different faces on a rectangular prism. Calculate each by multiplying the length by width, add the three results together and multiply by 2 to work out the total area.
Otherwise, you'd have to say the volume is 675x cubic units. Thus, the capacity of this tank is 73,287 cubic inches. Now connect the crosses (see Fig. 24c) with a straight line. The line indicates the growth rate of the plant; this is the height increase over time. After 1 week the height is 2 cm; this is indicated on the graph with A; after 2 weeks the height is 5 cm, see B, and after 3 weeks the height is 10 cm, see C, as shown in Fig.
The basic unit of area in the metric system is the square metre , which is obtained by multiplying a length of 1 metre by a width of 1 metre (see Fig. 9). The basic unit of length in the metric system is the metre . One metre can be divided into 10 decimetres , 100 centimetres or 1000 millimetres ; 100 m equals to 1 hectometre ; while 1000 m is 1 kilometre . In the case of a square or a rectangle, the expression length is commonly used instead of base and width instead of height. In the case of a circle the expression diametre is used (see Fig. 1b). It is important to be able to measure and calculate surface areas.
It might be necessary to calculate, for example, the surface area of the cross-section of a canal or the surface area of a farm. If the shallow end is 3 feet and the deep end is 9 feet, and assuming the slope of the pool bottom is gradual and even, then the average depth is 6 feet. More complicated pool shapes will require multiple calculations and adding them together.
For more detailed information on the calculations, read more below the calculator. For additional help, contact a swimming pool professional. We all know that the volume is calculated by multiplying Width x Height x Length or Area of the end x Length. Find the volume of one cube, then multiply that by the number of cubes.